در این مطلب به مفاهیم اساسی Logistic Regression و اینکه در حل چه نوع مسائلی می‌تواند به ما کمک کند،خواهیم پرداخت.

Logistic Regression یک الگوریتم طبقه‌بندی است که برای تخصیص مشاهدات به مجموعه‌ای گسسته از کلاس‌ها استفاده می‌شود.

برخی از نمونه‌های مسائل طبقه‌بندی عبارتند از: ایمیل هرزنامه یا عدم هرزنامه، تراکنش‌های آنلاین تقلب یا عدم تقلب، تومور بدخیم یا خوش‌خیم.   Logistic Regression خروجی خود را برای تبدیل به یک مقدار احتمالی با استفاده از تابع سیگموئید لجستیک نشان می‌دهد.

انواع Logistic Regression چیست؟

1. باینری (مثلاً تومور بدخیم یا خوش خیم).
2. توابع چند خطی با شکست در کلاس (مانند گربه، سگ یا گوسفند).

Logistic Regression

Logistic Regression یک الگوریتم یادگیری ماشین است که برای مسائل طبقه بندی استفاده می‌شود، یک الگوریتم تحلیل پیش بینی و بر اساس مفهوم احتمال است.

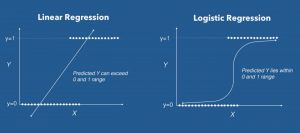
ما می‌توانیم Logistic Regression را یک مدل رگرسیون خطی بنامیم، اما Logistic Regression از یک تابع هزینه پیچیده‌تر استفاده می‌کند، این تابع هزینه را می‌توان به‌عنوان «تابع سیگموید» یا به‌جای یک تابع خطی به‌عنوان «تابع لجستیک» تعریف کرد.

فرضیه Logistic Regression به آن تمایل دارد که تابع هزینه را بین 0 و 1 محدود کند. بنابراین توابع خطی نمی‌توانند آن را نشان دهند زیرا می‌تواند مقداری بزرگتر از 1 یا کمتر از 0 داشته باشد که طبق فرضیه Logistic Regression امکان‌پذیر نیست.

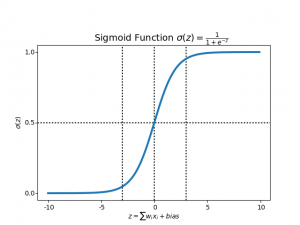
تابع سیگموئید چیست؟

برای ترسیم مقادیر پیش‌بینی‌شده به صورت احتمالاتی، از تابع Sigmoid استفاده می‌کنیم. تابع هر مقدار واقعی را به مقدار دیگری بین 0 و 1 ترسیم می‌کند. در یادگیری ماشین، ما از سیگموید برای ترسیم پیش بینی ها به صورت احتمالات استفاده  می‌کنیم.

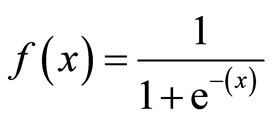
بازنمایی فرضیه

هنگام استفاده از رگرسیون خطی، از فرمول فرضیه استفاده کردیم.

hΘ(x) = β₀ + β₁X

برای Logistic Regression می‌خواهیم کمی آن را اصلاح کنیم.

σ(Z) = σ(β₀ + β₁X)

ما انتظار داریم که فرضیه ما مقادیری بین 0 و 1 بدهد.

Z = β₀ + β₁X

hΘ(x) = sigmoid(Z)

i.e. hΘ(x) = 1/(1 + e^-(β₀ + β₁X)

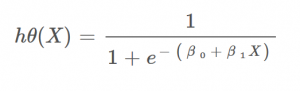
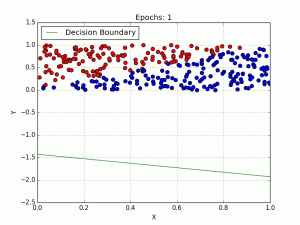
مرز تصمیم‌گیری

زمانی که ورودی ها را از یک تابع پیش‌بینی عبور می‌دهیم و امتیاز احتمالی بین 0 تا 1 برمی گرداند، انتظار داریم طبقه بندی کننده ما مجموعه ای از خروجی ها یا کلاس ها را بر اساس احتمال به ما بدهد.

به عنوان مثال، ما 2 کلاس داریم، بیایید آنها را مانند گربه ‌ها و سگ‌ها در نظر بگیریم (1 – سگ، 0 – گربه). ما اساساً با یک مقدار آستانه تصمیم می گیریم که بالاتر از آن مقادیر را در کلاس 1 طبقه بندی کنیم و مقدار آن به زیر آستانه برود سپس آن را در کلاس 2 طبقه بندی کنیم.

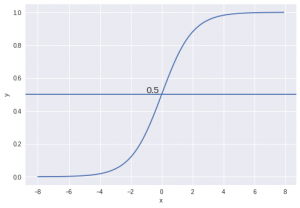
همانطور که در نمودار بالا نشان داده شده است، آستانه را 0.5 انتخاب کرده ایم. اگر تابع پیش بینی مقدار 0.7 را برگرداند، این مشاهدات را به عنوان کلاس 1 (DOG) طبقه بندی می‎‌کنیم. اگر پیش‌بینی ما مقدار 0.2 را برگرداند، مشاهده را به عنوان کلاس 2 (CAT) طبقه‌بندی می‌کنیم.

تابع هزینه

ما در مورد تابع هزینه J(θ) در رگرسیون خطی یاد گرفتیم، تابع هزینه نشان دهنده هدف بهینه سازی است. یعنی ما یک تابع هزینه ایجاد می‌کنیم و آن را به حداقل می‌رسانیم تا بتوانیم یک مدل دقیق با حداقل خطا ایجاد کنیم.

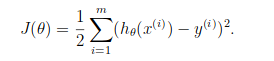
اگر بخواهیم از تابع هزینه رگرسیون خطی در “رگرسیون لجستیک” استفاده کنیم، فایده ای نخواهد داشت. زیرا در نهایت یک تابع غیرمحدب با مینیمم‌های محلی بسیار است، که در آن به حداقل رساندن مقدار بسیار دشوار است.

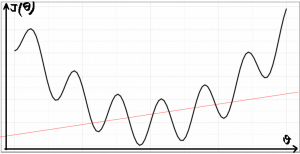
برای رگرسیون لجستیک، تابع هزینه به صورت زیر تعریف می‌شود:

log(hθ(x)) if y = 1

log(1−hθ(x)) if y = 0

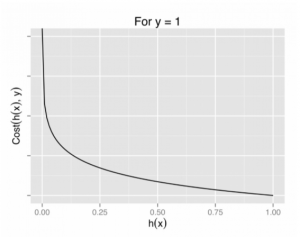
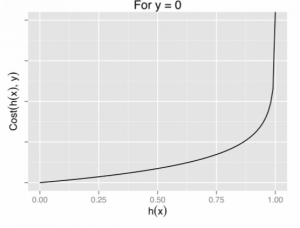
دو تابع فوق را می توان در یک تابع واحد فشرده کرد.

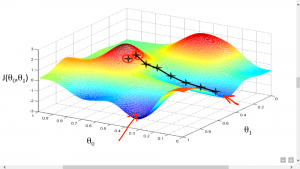
گرادیان نزولی

حال این سوال پیش می آید که چگونه مقدار هزینه را کاهش دهیم؟ خب، این را می‌توان با استفاده از Gradient Descent انجام داد. هدف اصلی گرادیان نزولی به حداقل رساندن مقدار هزینه است. یعنی min J(θ).

اکنون برای به حداقل رساندن تابع هزینه، باید تابع گرادیان نزولی را روی هر پارامتر اجرا کنیم.

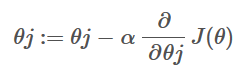
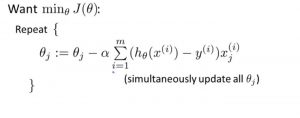
گرادیان نزولی تشبیهی دارد که در آن باید خودمان را در بالای دره کوه تصور کنیم و رها شده و چشم بسته بمانیم، هدف ما رسیدن به پایین تپه است. احساس شیب زمین در اطراف شما چیزی است که همه دارند. خب، این عمل مشابه محاسبه گرادیان نزولی است، و برداشتن یک گام مشابه یک تکرار از به‌روزرسانی پارامترها است.